一根打了结的橡皮筋，背后究竟隐藏着怎样的数学奥秘？

在三维空间中，一条闭合的曲线可以以无数方式缠绕、纽结。看似随手一扭的形状，却构成了现代数学中极其深邃的研究领域——纽结理论。而就在过去的几年里，一个长达二十余年的数学“共识”，在清华大学丘成桐数学科学中心的青年数学家高鸿灏手中被彻底推翻。

数学界曾普遍认为，一条纽结能容纳的“特殊几何结构”——拉格朗日填充数量应该极其有限。2022年，高鸿灏与合作者美国加州大学戴维斯分校教授罗杰·卡萨尔斯（Roger Casals）首次证明了存在无限多个拉格朗日填充，推翻了业内专家二十余年的错误猜测，创新性地使用了微局部层、丛代数理论，证明了大量勒让德链环都可以界定无穷多个拉格朗日填充。

2024年，他们又引入了新理论新技术，通过引入箭图及其势能函数工具，结合辛几何，证明了每一个丛代数种子均可以提升为拉格朗日填充，由此实现了填充猜想中满射的部分，给出了填充完备分类的下界，实现了填充分类的又一个重大突破，推进了拉格朗日填充的分类问题。

这一结论不仅颠覆了领域认知，更构建起一座跨越几何与代数的全新桥梁，为低维拓扑、辛几何与丛代数等多个方向的发展提出了新的理论框架，历经9个月审稿，成果发表于国际顶级数学期刊《数学新进展》，并被评为“2024年清华大学最受师生关注的年度亮点成果”之一，入选“2025年中关村论坛世界科技领先成就展”。2026年1月3日，凭借在拉格朗日填充分类问题上的突破性探索，高鸿灏在第十届世界华人数学家大会（ICCM2025）上荣获最佳论文奖。

高鸿灏（左二）在第十届世界华人数学家大会上荣获最佳论文奖

被低估的“无限”：当数学直觉第一次失效

要理解这一突破，可以从一个朴素的想象开始：设想一根钢丝被弯成一个环状的结，它的表面光滑而坚硬，那么在它所包围的空间内部，我们能否拉出一张膜，让这张膜的边恰好贴在钢丝上？这张膜就是数学意义上的“填充”。

然而数学家并不满足于任意一张膜，他们关心的是一种更稀有、更特殊的结构——拉格朗日填充。这种填充满足辛几何的严格条件，是高维空间中“运动”和“能量”最自然的形态。由于其要求极高，数学界长期认为这样的“特殊膜”应该非常稀缺。1990年代起，许多经典纽结都被证明只拥有有限数量的拉格朗日填充，进一步强化了这一直觉。

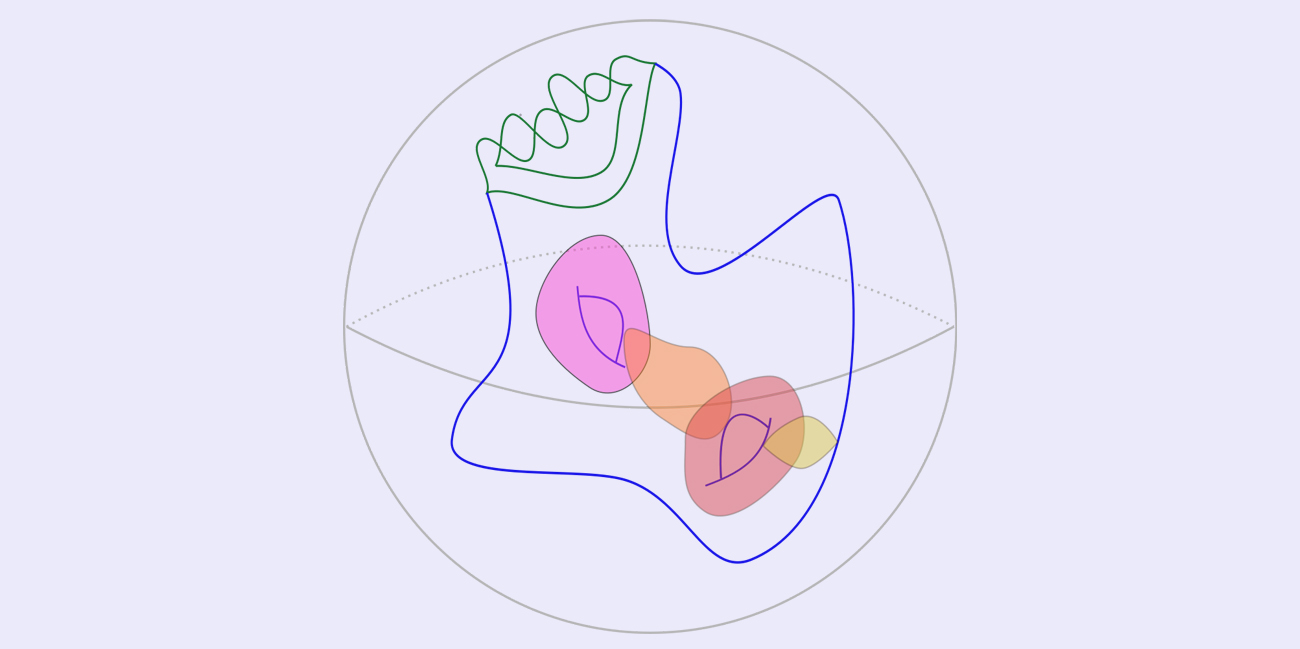
拉格朗日填充的一种形态

然而，在研究纽结的对称性时，高鸿灏与合作者罗杰·卡萨尔斯注意到了一种突破性的迹象：某些几何操作每一次施加都让生成的结构发生微妙但本质的变化。他们构造出两个基本的几何操作，记作 A 与 B，而它们的一个关键性质是——顺序不同，则结果不同。这在数学中是一个足以震动整个领域的信号：只要能排列出不同的操作顺序，就能制造出无穷多个彼此不同的拉格朗日填充。换句话说，数学界长期坚持的“有限性”假设，在这些看似普通的环面结上彻底失效。

更令人惊讶的是，这种无限并不是罕见的特例。随着技术的完善，高鸿灏与合作者发现：无限性并非偶发，而是广泛存在于各类纽结中。那些曾被认为“结构简单”“应当有限”的纽结，实际上往往拥有无限多种几何填充方式。这个发现直接改写了数学界的认知版图，促使研究者重新思考纽结几何的本质。

从几何走向代数：建立“有限与无限”真正的边界

如果说“构造出无限多种填充”是一束照进几何世界的光，那么更深刻的突破，则是高鸿灏与合作者找到了判断某个纽结是否具有无限多填充的根本依据。这个依据不来自几何的形状，而来自代数结构的分类。

拉格朗日填充（图左）与其对应的丛代数种子（图右）

过去十年，丛代数（cluster algebra）成为现代代数的关键工具。它以“箭图”的形式记录代数关系，并将不同的代数结构划分为两类：ADE 类型（有限型）与非 ADE 类型（无限型）。在数学中，ADE 类型常常代表着非常特殊、对称性极强、数量有限的结构，被视为“稀有的秩序”。令人震惊的是，当高鸿灏与合作者将纽结的几何数据与丛代数对应起来时，他们发现：决定拉格朗日填充是有限还是无限的，恰恰就是这个古老的分类。

也就是说，纽结的几何结构中隐藏着一个纯代数的灵魂。只要它对应的箭图不属于 ADE 型，那么它必然有无限多种拉格朗日填充；反之，如果是 ADE 型，它的填充数量就被严格限制在有限范围内。每一次纯代数的灵魂能够找到对应的几何表达，都在国际数学界产生轰动，而这次更是如此激动人心。

然而，要让这一对应真正成立，还需突破一个关键难题。几何构造往往无法直接忠实模仿代数变换，原因是几何对象在变换过程中可能出现自相交——两个部分撞在一起，导致几何结构被破坏。为了解决这一问题，高鸿灏引入了“带势能的箭图”技术。势能函数的存在像一张标注风险的地形图，提前指出可能发生碰撞的位置，使得几何的变形可以绕开危险区域。最终他们证明，代数世界中的每一个“种子”，都能在几何世界中至少找到一个对应的拉格朗日填充。这意味着代数中的“无限多”，几何中也真实存在“无限多”。

这项成果不仅给出了严格的理论解释，更奠定了一个方向：未来有可能建立起几何填充与代数对象的“一一对应”。这将使数学家能够依靠代数计算来理解复杂几何，为辛几何与低维拓扑打开全新的研究路径。

在纯粹中前行：年轻数学家的探索与未来

数学史上的每一次重大推进，都来自研究者对抽象问题的长期坚持。相比那些能立即看到应用前景的领域，辛几何和纽结理论显得更加孤独，也更加纯粹，其魅力在于探索本身。高鸿灏认为，真正驱动数学家前行的是“对问题本身的热爱”。

他坦言，许多关键性的构想来自对结构的直觉式感应，而这种直觉往往需要长时间的积累。构造无限多填充的想法最初并不宏大，只是反复观察几何操作后的某种不对称感；而丛代数的引入，也不是一开始就显而易见，而是在试图解释操作模式时自然出现的线索。“数学研究不是执着地去证明对错，而是一个不断探索的过程。”他说。

高鸿灏与学生讨论交流

本科毕业于香港科技大学，博士毕业于美国西北大学的高鸿灏，曾先后于法国傅立叶研究所、美国密歇根州立大学从事博士后研究工作。2022年，他做出一个重要的人生抉择——回国加入清华大学丘成桐数学科学中心。这一选择，源于他对中心与求真书院发展理念的深度认同，更源于他学成报国、矢志不渝的历史使命感。

如今，高鸿灏的学术研究在国际同行中获得认可。同时，他也将大量时间投入教学与人才培养。高鸿灏常鼓励学生们探索那些鲜有人关注的研究方向，用热爱点亮学术道路。

高鸿灏作为班主任代表发言

谈及中国数学的未来，他充满信心。在他看来，中国年轻学者正在越来越多地站在科学研究的世界前沿上。大量针对基础研究的投入，更加开放的国际合作，也让中国数学在过去十年呈现前所未有的活力，特别是在几何与代数的交叉领域，中国团队已具备形成原创体系的潜力。

在这些探索与期待中，那些原本被视为“不可能”的无限，正在被重新理解。而在纽结深处，被遮蔽许久的几何可能性，正被一位青年数学家与他的学生们一点点照亮。