清华新闻网5月20日电 弹性结构中的突跳失稳（snap-through buckling）是一类典型的非线性失稳现象，广泛存在于自然界与工程系统中。例如，捕蝇草叶片通过突跳闭合捕捉猎物，雨伞在强风中突然翻转，均体现了系统在双稳态结构间的快速切换特征。这种高效的形状切换与能量转换机制，使突跳失稳在微机电开关、跳跃机器人、可编程材料与能量收集装置等领域展现出巨大的应用潜力。

在力学模型中，欧拉屈曲为双稳态行为的研究提供了经典范式。细长的弹性条带在轴向压缩下会自然屈曲至向上或向下两个对称的稳定构型之一（图1）。尽管系统在几何形状、边界条件和激励方式上具备完美的左右对称性，其在两种构型间切换的路径却常常表现为不对称。这一现象源于非对称路径具有更低的能量势垒，因此成为系统的自然选择。该矛盾揭示了自然界的深层规律：对称性破缺虽可降低能量势垒，却往往以牺牲工程应用所需的可控性为代价。尽管理论预测对称模态的存在，但传统加载方式下，对称路径如同隐匿于能量地貌中的“孤岛”，难以在准静态条件下被可靠触发。

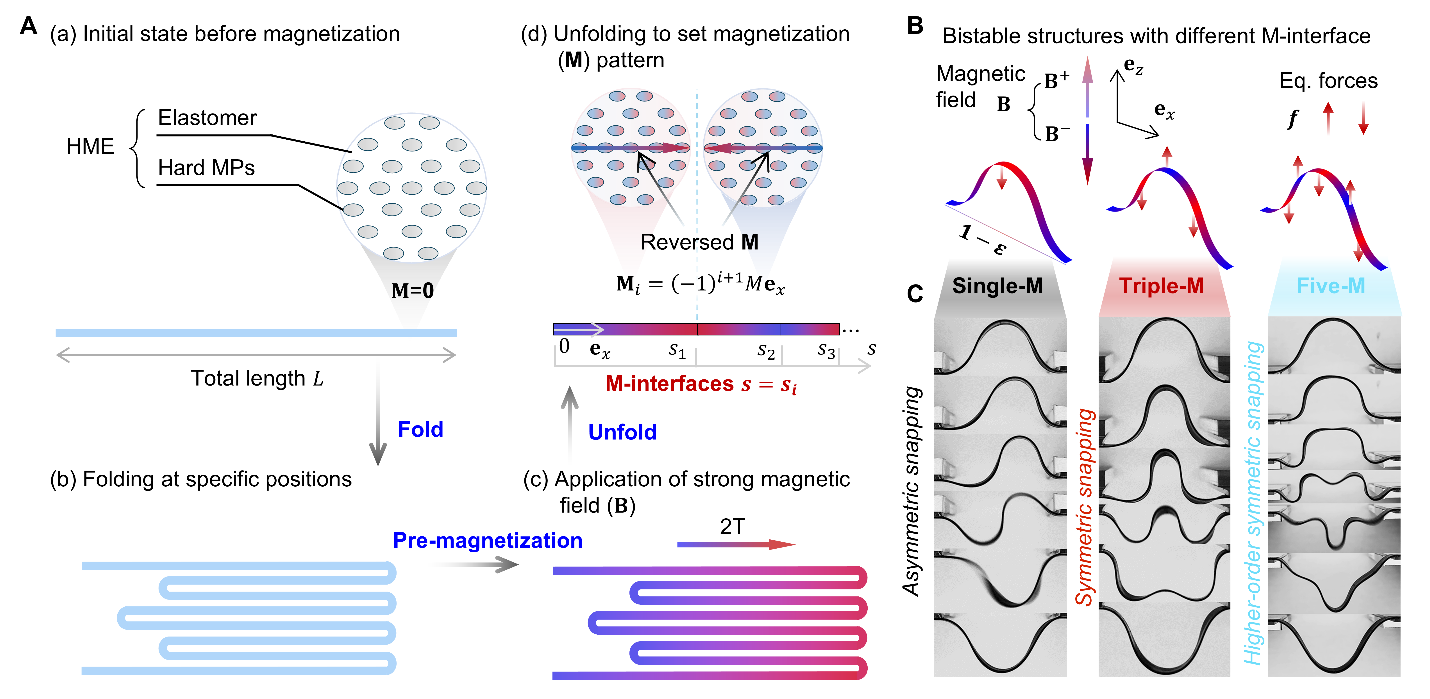
图1.“磁化界面”（M-interfaces）设计策略及其在不同突跳失稳模态中的实验实现，包括非对称模态、对称模态和高阶对称模态

针对这一挑战，清华大学航天航空学院张迎超副研究员、力学与工程交叉研究院高华健院士和俞璟副教授联合其他研究者创新性地引入了“磁化界面”（M-interfaces）设计理念，在硬磁弹性体结构中预设交替磁化区域，使结构在外加磁场作用下形成一系列方向交错的等效力对（图1）。该构型在保持系统本征对称性的基础上，构建了内部“力场博弈机制”：驱动力诱导结构发生突跳失稳，等效阻力则有效抑制非对称模态的生成。借助这一“分布式调控”策略，研究团队首次在准静态条件下实现了对称性突跳失稳路径的稳定激发，并建立了适用于更复杂双稳系统的通用设计方法。

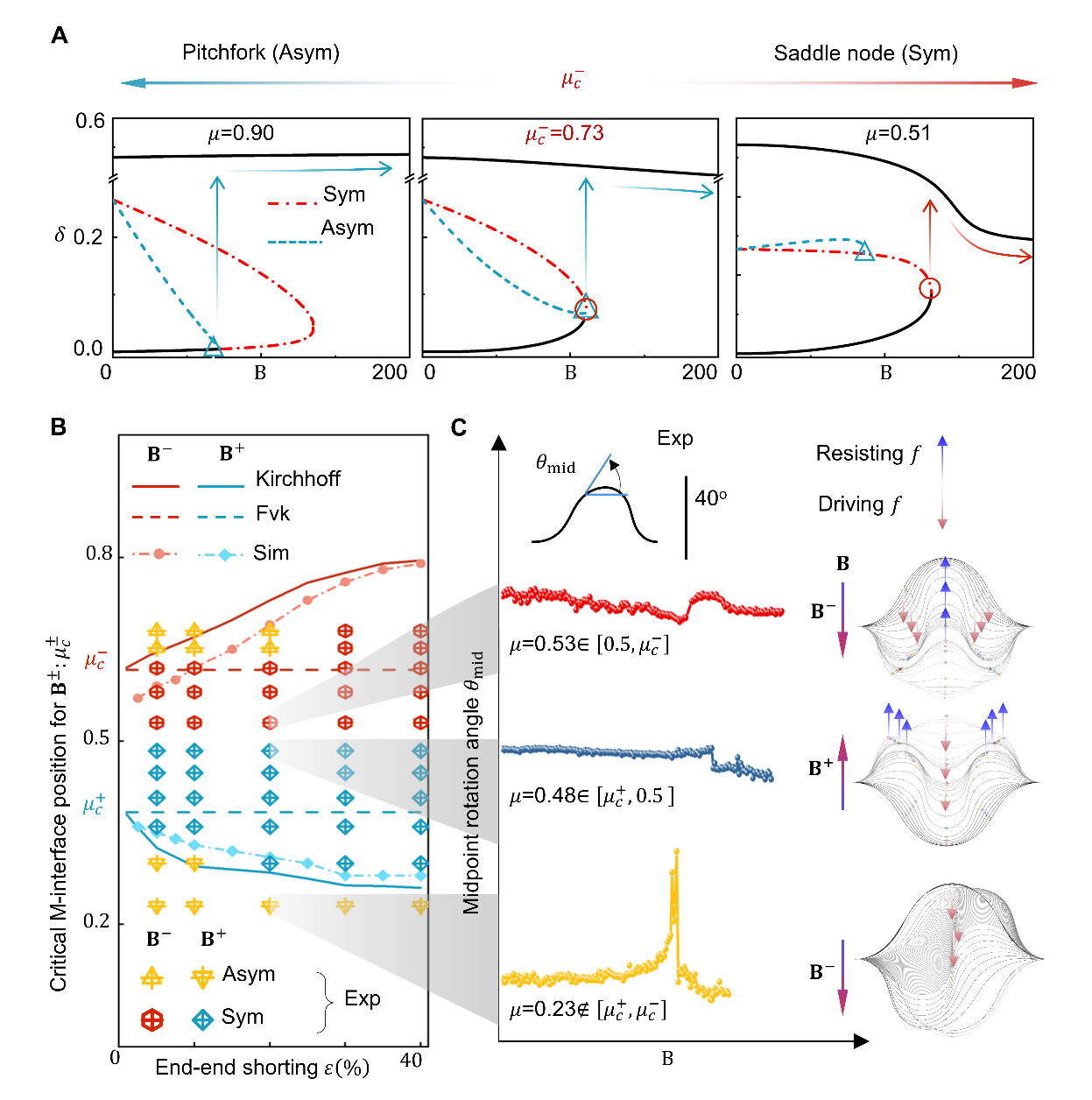
图2.以三界面系统为例揭示对称与非对称模态的竞争机制，以及理论预测与仿真、实验对比

研究以三界面系统（Triple-M）为例（图2），进一步揭示了其背后的力学原理：对称与非对称模态的竞争源于叉式分岔（pitchfork bifurcation）与鞍结分岔（saddle-node bifurcation）的主导先后关系。随着磁化界面参数接近临界值，非对称路径变得“刚性不可及”，鞍结分岔先于叉式分岔发生，系统自然转入对称模式。基于这一机制，研究团队基于五界面（Five-M）系统（图3），构建了完整的“突跳相图”，明确界面参数与结构失稳行为之间的对应关系。该方法不仅实现了准静态条件下的低阶对称突跳，还进一步诱导出高阶对称形态，并揭示了不同阶次之间临界磁场的准线性标度律关系，为复杂双稳态系统的精确控制提供了理论基础和设计依据。

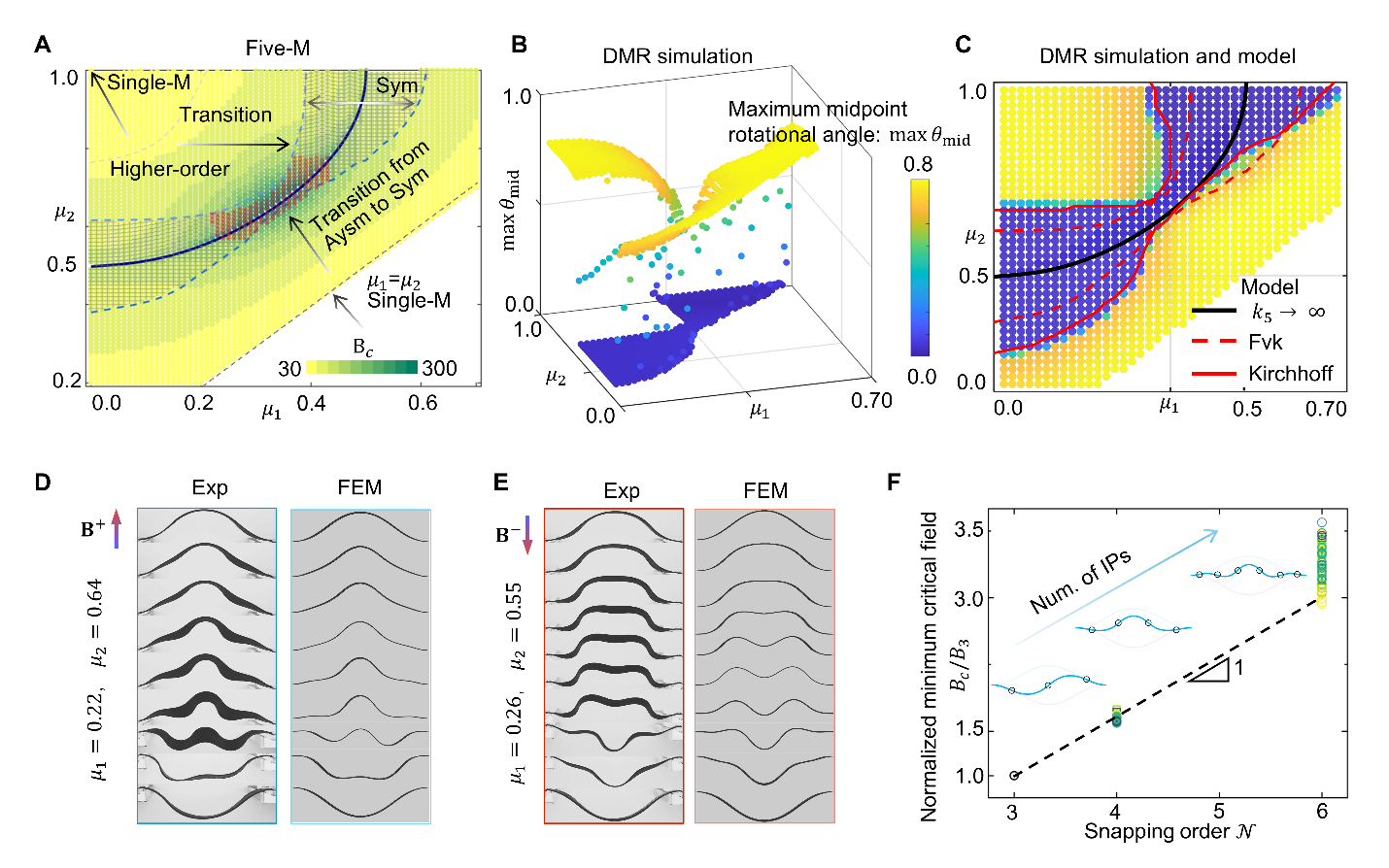
图3.基于五界面系统构建“突跳相图”，明确磁化界面参数与结构突跳失稳行为之间的对应关系，揭示不同阶次之间临界磁场的准线性标度律关系

相关研究成果以“磁驱动设计实现对称性突跳失稳”（Achieving symmetric snap-through buckling via designed magnetic actuation）为题，于5月14日发表于《科学进展》（Science Advances）。

高华健和俞璟为论文共同通讯作者，张迎超为论文第一作者。论文的其他合作者包括英国纽卡斯尔大学（Newcastle University）助理教授黄炜成、英国伯明翰大学（University of Birmingham）助理教授刘明超。研究得到清华大学启动基金、新加坡国家研究奖金（Singapore National Research Fellowship）的支持。

论文链接：

https://www.science.org/doi/10.1126/sciadv.adw1259

供稿：航院

编辑：李华山

审核：郭玲